Floyd算法又称为弗洛伊德算法,插点法,是一种用于寻找给定的加权图中顶点间最短路径的算法算法过程1,从任意一条单边路径开始所有两点之间的距离是边的权,或者无穷大,如果两点之间没有边相连2,对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更。
不同算法适用于不同的场景,如Dijkstra算法适用于确定起点的最短路径问题,Floyd算法适用于全局最短路径问题等 在选择算法时,需根据具体问题的特点和图的性质进行综合考虑。
最短路径的算法主要有三种floyd算法Dijkstra算法BellmanFord贝尔曼福特一floyd算法 基本思想如下从任意节点A到任意节点B的最短路径不外乎2种可能,1是直接从A到B,2是从A经过若干个节点X到B所以,我们假设DisAB为节点A到节点B的最短路径的距离,对于每一个节点X,我们检查DisAX。
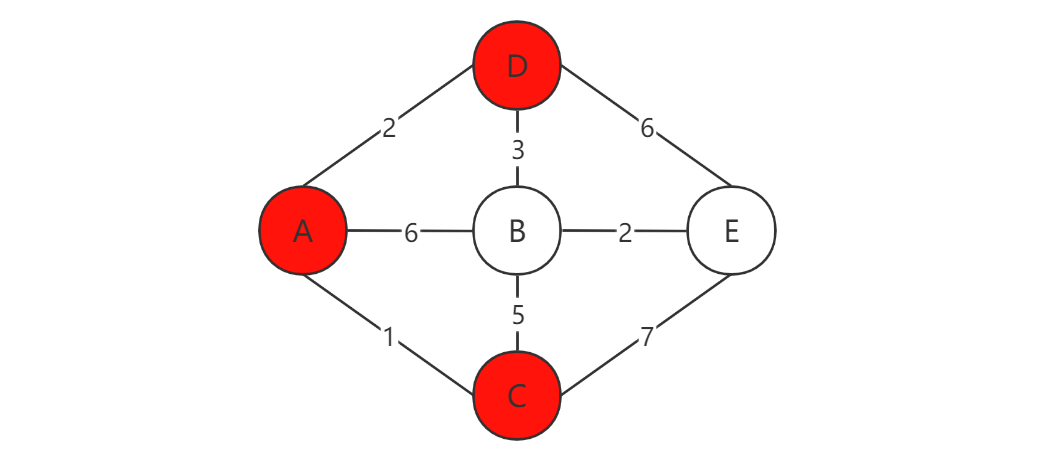
Floyd算法,又称插点法,是一种动态规划策略,旨在寻找加权图中多源点之间的最短路径,与Dijkstra算法有相似之处该算法源于斯坦福大学计算机科学系教授Robert Floyd,dijkstra算法floyd区别他于1978年荣获图灵奖FloydWarshall算法特别适用于处理具有正或负权重边但无负周期的图,它能一次性找到所有顶点对之间的最短路径。
dijkstra算法是计算单源最短路径也就是只有一个源点,到各个点的最短路径 floyd算法是多源最短路径,计算的是各个点之间的最短路径。
无负权的话当然也不能有环的时候,我是这么理解的Dijkstra因为用优先队列去维持,所以速度还可以 Floyd的话,其实对于大多数情况,算法很快就收敛dijkstra算法floyd区别了,甚至有时候一次就搞定了这个就很神奇所以有些迭代不是有必要地,虽然分析是说复杂度是V^3之类的吧我觉得这些复杂度分析也不。
Floyd算法是一种针对All Pairs Shortest Paths APSP问题的动态规划方法,特别适合处理稠密图,其边权可以是正数也可以是负数这个算法以其简洁高效而著称,其核心是紧凑的三重循环结构,对于包含大量边的图,相对于独立执行V次Dijkstra算法,其效率有着明显的优势首先,Floyd算法的一大优点是其直观。




























































































































































































































































































































































































































































































































网友评论
最新评论