矩阵等价和相似区别矩阵相似与等价的区别的是性质不同特点不同1性质不同 矩阵等价在线性代数和矩阵论中矩阵相似与等价的区别,有两个m×n阶矩阵A和B,如果这两个矩阵满足B=QAPP是n×n阶可逆矩阵,Q是m×m阶可逆矩阵,那么这两个矩阵之间是等价关系也就是说,存在可逆矩阵,A经过有限次的初等变换得到B矩阵相似在线性。
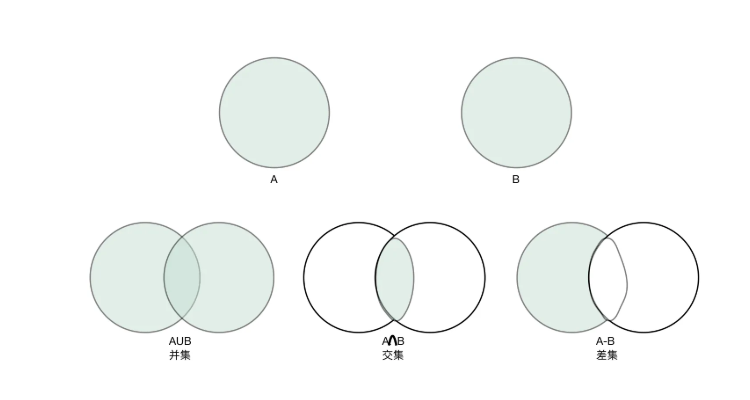
一矩阵等价相似和合同之间的区别1等价,相似和合同三者都是等价关系2矩阵相似或合同必等价,反之不一定成立3矩阵等价,只需满足两矩阵之间可以通过一系列可逆变换,也即若干可逆矩阵相乘得到4矩阵相似,则存在可逆矩阵P使得,AP=PB5矩阵合同,则存在可逆矩阵P使得,P^TAP=B6。
等价通常是指两个矩阵可以通过初等变换互相转换,这只需两个矩阵的秩相同即可这是一个较为宽松的条件,应用范围有限矩阵A相似于矩阵B,则存在一个非奇异矩阵P,使得PAP1=B这是高等代数中最重要的关系,相关理论占据矩阵相似与等价的区别了课程的一半左右相似关系可以推出等价关系矩阵合同则较为类似,但要求存在一。
这就证实矩阵相似与等价的区别了它们的等价关系当两个同型矩阵A和B的秩相等时,它们也一定是等价的然而,相似关系比等价更强,因为它不仅要求秩相等,还要求存在更直接的矩阵关系总的来说,相似性比等价性包含更多的矩阵特性,如特征值和行列式的共性因此,相似性是等价性的深化和扩展。
矩阵相似与合同之间不存在充要关系,存在相似但不合同的矩阵,也存在合同但不相似的矩阵这表明在矩阵理论中,相似与合同是两个相互独立但又相互关联的概念综上所述,相似关系强调了矩阵间的结构等价性,合同关系则强调了特定变换下的等价性,而等价关系则提供了更为广泛和基础的等价框架这三者在矩阵。
等价关系强调矩阵的秩相等它意味着矩阵在保持线性空间基本维度不变的情况下,可以相互转换,即使它们在细节上有所不同等价关系下的矩阵,其线性变换性质保持了整体结构的相似性,尽管它们在特定线性空间的表示形式可能不同综上,合同关系侧重于特征值的正负数量匹配,相似关系则要求特征值相同且矩阵能。
在数学领域,矩阵之间的关系被广泛探讨,特别是相似和等价的概念合同和相似这两个术语,常常被用来描述矩阵之间的关系合同,意味着矩阵可以通过合同变换来相互转换相似,则表示矩阵之间可以通过相似变换实现转换值得注意的是,合同关系可以推出相似关系,但相似关系不一定能推出合同关系具体来说,如果。
区别1性质不同 如果矩阵A与矩阵B的任何一处特征相同,那么就可以称矩阵A与B相似而只有当矩阵A与矩阵B所有的特征完全相同完全吻合的情况下,才可称之为矩阵A与矩阵B等价2特点不同 矩阵A与B相似的特点是具有传递性与对称性,而矩阵A与B等价的特点是具有全等性。
值得注意的是,与单位矩阵相似的n阶矩阵仅限于单位阵E本身,与数量矩阵kE相似的n阶方阵仅限于数量阵kE本身同时,有相同特征多项式的矩阵不一定相似,这加深了相似与合同等价关系的理解难度综上所述,矩阵的相似合同等价关系在数学领域中扮演着重要角色掌握它们的定义性质与区别,将为考研。
合同与相似在矩阵性质上具有一定的联系合同关系强调矩阵间的线性变换,而相似关系则关注矩阵表示的等价性尽管存在一定的相似之处,但它们各自侧重的方面并不相同在矩阵理论中,合同与相似概念的区分十分重要合同更多涉及矩阵的线性变换特征,而相似强调矩阵的表示等价理解这两个概念之间的差异,对于。
本文旨在引导同学们从宏观视角理解和应用矩阵等价合同和相似的概念,而非局限于公式记忆首先,这三个概念之间的关系是等价矩阵的秩相等,而合同和相似的秩也必然相等,等价是最基础的性质矩阵等价,就好比解析几何中的坐标变换,虽然变换后的坐标不同,但长度不变,它表示矩阵经过初等变换后不影响。
1矩阵等价 矩阵A与B等价必须具备的两个条件1矩阵A与B必为同型矩阵不要求是方阵2存在s阶可逆矩阵p和n阶可逆矩阵Q, 使B= PAQ2矩阵A与B合同 必须同时具备的两个条件1 矩阵A与B不仅为同型矩阵而且是方阵2 存在n阶矩阵P P^TAP= B3矩阵A与B相似 必须同时。

A与B在等价矩阵下相似,当且仅当存在一个可逆矩阵P,使得P^1 * A * P = B以下是具体解释相似矩阵的定义如果存在一个可逆矩阵P,使得P^1 * A * P = B,那么称矩阵A与B相似这是判断两个矩阵是否相似的唯一标准等价矩阵与相似矩阵的区别等价矩阵的定义更为宽泛,如果存在两个可逆。
这意味着它们具有相同的特征值和相同的行列式值相似矩阵的行列式相等,但它们的迹不一定相等这与等价矩阵是不同的在等价的定义中,关注的是能否通过初等变换相互转化,而不是它们的线性映射或线性变换的特性然而在实际应用中,相似的矩阵在很多场合都是等价的通过理解这些概念之间的区别和联系。
关系对于实对称矩阵,合同关系与它们的正负惯性指数和标准型下的特征值有关相似矩阵的秩正负惯性指数和特征值相同,意味着它们既相似又合同综上所述,矩阵的相似等价正交和合同关系在数学和线性代数中具有不同的定义和性质,这些关系在矩阵理论数值计算优化问题等领域有着广泛的应用。



























































































































































































































































































































































































































































































网友评论
最新评论