极值和最值都是数学中用来描述函数或集合中最值和极值的区别的特殊值的概念最值和极值的区别,但它们有着不同的含义和用途1 极值extrema极值是指函数在某个区间或集合上取得的最大值或最小值极值分为两种类型最大值和最小值 最大值maximum函数在某个区间或集合上取得的最大值称为最大值记作fx =。
极值与最值概念不同,极值是与两侧相比的局部最大或最小值,而最值是定义域或指定区间内的最大或最小值极值与最值的关系是局部与整体的关系,极值是局部最大或最小值,最值是整体最大或最小值极值点是横坐标概念,极值点数量可能不止一个,且端点函数值不是极值极值是局部性质,与函数在。
极值和最值是数学中常用的概念,用于描述函数或数列中的最大值或最小值区别1 极值是指函数在某个特定的点上取得的最大值或最小值,而最值是指函数在整个定义域范围内取得的最大值或最小值2 极值是局部性质的,只考虑函数在某个点附近的取值情况而最值是全局性质的,考虑函数在整个。
定义不同,存在性不同等定义不同极值是一个函数的极大值或极小值,即一个函数在一点处的值大于或小于其邻域内其他各点的函数值而最值则是函数在定义域内的最大值或最小值,即一个函数在整个定义域上的最高点和最低点的函数值,是包含在极值内的存在性不同一个函数可能存在多个。
极值和最值的区别主要在于它们的概念和应用范围不同以下是详细信息1极值是指函数在其定义域内的某一点处取得的最大值或最小值,它是局部的概念,与该点附近的函数值进行比较,如果函数在该点处的值大于或等于其邻域内其他所有点的函数值,则该点为极大值如果函数在该点处的值小于或等于其。
从上面的定义最值和极值的区别我们可以看出,函数的极值和最值的主要区别在于极值是函数在某一点的局部性质,而最值是函数在整个定义域上的全局性质极值只要求函数在某一点的值大于或小于其附近任意一点的值,而最值要求函数在某一点的值大于或小于其定义域上所有其他点的函数值极值可能存在多个,而最值只能有一个。
概念不同极值是与它的两侧相比,大于两侧是极大值,小于两侧是极小值最值则是函数在定义域或指定区间内的最大最小值除特定函数,两者无必然联系极值与最值的关系是局部与整体的关系一般来说,最值是全局最优解,极值是局部最优解。
同理也定义最值和极值的区别了极小值概念而最值是一个全局概念,在某区间上某点的函数值比这个区间内的所有函数值都大,那么它就是最大值,同理,也可以定义最小值概念如果在某闭区间内的函数的最大值,一定是极大值或者端点函数值中的一个最小值也是极小值和端点函数值中的一个。

在数学的范畴中,当我们探讨函数性质时,一个重要的概念是极值和最值,它们是理解函数行为的关键点极值function fx在点x#8320的局部表现lt,如同一个山峰或山谷的顶点,是在给定的去心领域内,函数值相对于其两侧的局部最大或最小请注意,极值并不必然意味着是最值lt,因为它可能只是。
区别在于二者概念不同极值是与它的两侧相比,大于两侧是极大值,小于两侧是极小值最值则是函数在定义域或指定区间内的最大最小值除特定函数,两者无必然联系联系一些情况下,函数有极值无最值另一些情况下,函数有最值无极值,还有一些情况下,最值 = 极值极值是一个函数的极大值或。
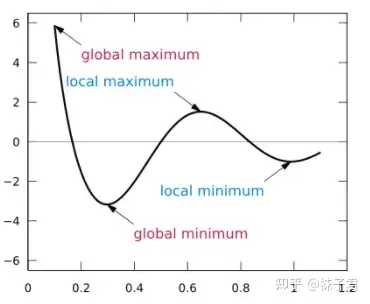
极值是在某一特定区间中,函数先增后减是极大值,先减后增是极小值最值是在区间中的最大或最小值,即函数图中的最高点或最低点。






































































































































































































































































































































































































































































































网友评论
最新评论